2022-09-26 16:09:10 玉溪华图考试网 http://yuxi.huatu.com/ 文章来源:玉溪华图

国考备考群
玉溪华图小编为您整理国家公务员考试备考文章:2023国家公务员考试大纲原文
2023年国家公务员考试大纲暂未发布,历年国家公务员考试公告都在10月中旬左右发布,在国家公务员局发布。
| 历年国家公务员考试时间安排表 | |||||||
| 年份 | 公告发布时间 | 报名时间 | 资格审查 | 确认/缴费时间 | 打印准考证 | 笔试时间 | 成绩查询 |
| 2022 | 2021.10.14 | 10月15日-24日 | 10月15日-26日 | 11.1日-7日 | 11.22日-28日 | 11月28日 | 2021年1月1日 |
| 2021 | 2020.10.14 | 10.15日-24日 | 10.15日-26日 | 11.1日-7日 | 11.23日-29日 | 11月29日 | 2021年1月10日 |
| 2020 | 2019.10.14 | 10.15日-24日 | 10.15日-26日 | 10.31日-11.6日 | 11.18日-24日 | 11月24日 | 2020年1月7日 |
| 2019 | 2018.10.21 | 10.22日-31日 | 10.22日-11.2日 | 11.8日-14日 | 11.26日-12.2日 | 12月2日 | 2019年1月17日 |
| 2018 | 2017.10.28 | 10.30日-11.8日 | 10.30日-11.10日 | 11.17日-11.22日 | 12.4日-10日 | 12月10日 | 2018年1月24日 |
| 2017 | 2016.10.13 | 10.15日-24日 | 10.15日-26日 | 11.2日-7日 | 11.21日-27日 | 11月27日 | 2017年1月9日 |
| 2016 | 2015.10.13 | 10.15日-24日 | 10.15日-26日 | 11.2日-7日 | 11.23日-29日 | 11月29日 | 2016年1月29日 |
| 2015 | 2014.10.13 | 10.15日-24日 | 10.15日-26日 | 11.2日-7日 | 11.24日-29日 | 11月30日 | 2015年1月10日 |
| 2014 | 2013.10.14 | 10.16日-24日 | 10.16日-26日 | 11.2日-7日 | 11.18日-23日 | 11月24日 | 2014年1月6日 |
| 2013 | 2012.10.12 | 10.15日-24日 | 10.15日-26日 | 11.2日-7日 | 11.19日-24日 | 11月25日 | 2013年1月7日 |
| 2012 | 2011.10.13 | 10.15日-24日 | 10.15日-26日 | 11.2日-7日 | 11.24日-29日 | 11月27日 | 2012年1月8日 |
| 2011 | 2010.10.11 | 10.15日-24日 | 10.15日-26日 | 11.2日-7日 | 11.23日-28日 | 12月5日 | 2011年1月中旬 |
| 2010 | 2009.10.12 | 10.15日-24日 | 10.15日-26日 | 11.2日-7日 | 11.23日-28日 | 11月29日 | 2010年1月12日 |
以上这些就是大连华图老师为大家分享的2023云南国家公务员考试文章:2023国家公务员考试大纲原文,期待大家继续关注同类话题的学习!
行测干货数量关系解题方法之赋值法
在每年的考试中,我们数量关系这个模块会有多道基础应用题,这些题目有些正向直接求解比较困难,这时就需要我们用一些 特殊的方法比如赋值法来进行计算,只要我们能够掌握赋值法的应用特征以及赋值原则,就能帮助大家提高做题速度,从而帮助我们在 考场上节省时间。
一、题型特征
题干含中有A=B×C的形式。
题干中有分数、百分数、比例、倍数等。
二、常用题型
工程问题、行程问题、溶液问题、经济利润问题
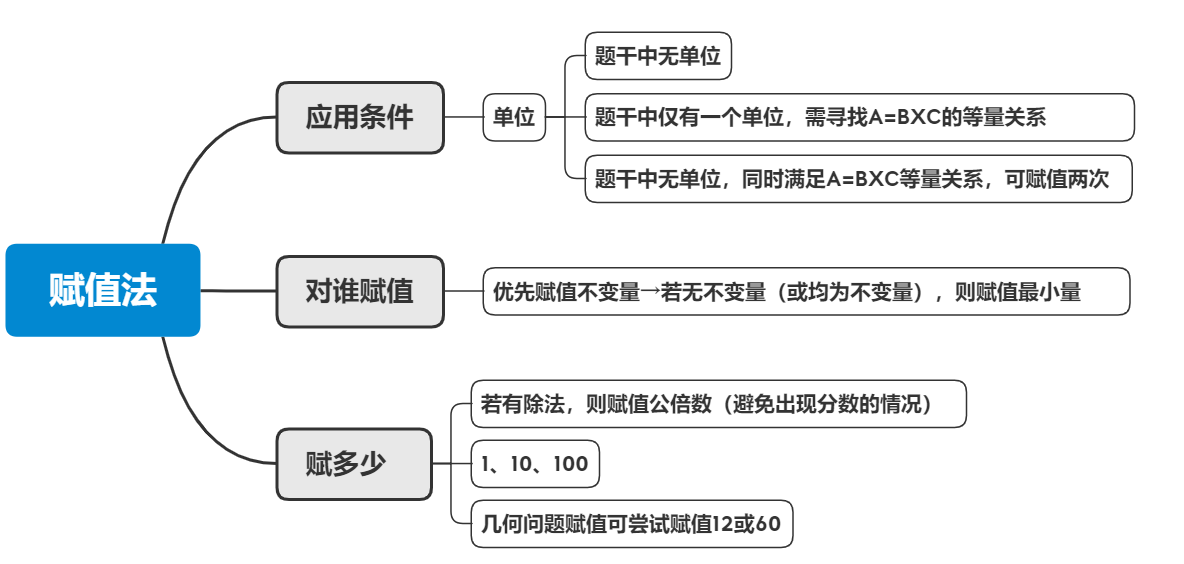
三、赋值原则
1.A=B×C中:
优先赋值总量A(一般A为不变量);赋成B或C的公倍数。
A变化,则赋值B或C(存在比例关系优先);B或C按比例赋值
2.A=B×C中,无具体值,仅有比例关系,赋值两次。
三、知识应用
(2019联考)某楼盘的地下停车位,第一次开盘时平均价格为15万元/个;第二次开盘时,车位的销售量增加了一倍、销售额增加 了60%。那么,第二次开盘的车位平均价格为:
A. 10万元/个 B. 11万元/个
C. 12万元/个 D. 13万元/个
【答案】C
【解析】
第一步,本题考查基础公式类经济利润问题,用赋值法解题。
第二步,销售额=平均价格×销售量,已知第一次开盘平均价格为15万元/个,赋销售量为1,则销售额为15万。第二次开 盘时,销售量增加了一倍,即为2,销售额增加了60%,得销售额为15×(1+60%)=24(万元),故第二次开盘平均价格为 24÷2=12(万元/个)。
因此,选择C选项。
(2014四川)某钢厂生产一种特种钢材,由于原材料价格上涨,今年这种特种钢材的成本比去年上升了20%。为了推销该种钢材, 钢铁厂仍然以去年的价格出售,这种钢材每吨的盈利下降40%,不过销量比去年增加80%,那么今年生产该种钢材的总盈利比去年增加了 多少?
A. 4% B. 8%
C. 20% D. 54%
【答案】B
【解析】
第一步,本题考查经济利润问题,属于利润率折扣类,用赋值法解题。
第二步,总利润=单利润×销量,根据“盈利下降40%”,赋值去年每吨利润为10,可得今年每吨盈利为 10×(1-40%)=6;根据“销售量比去年增加了80%”,赋值去年销售量为10,可得今年销售量10×(1+80%)=18,故 去年总盈利为10×10=100,年总盈利为6×18=108。
第三步,今年总盈利比去年增加(108-100)/100=8%。
因此,选择B选项。
(2019联考)2016年某电子产品定价为n元/台,2017年由于技术升级成本降低,定价降低10%。每台产品利润提升10%,2017年全 年销售这种产品的总利润较2016年增加了21%,2017年的销量比2016年:
提升了不到20% B. 提升了20%或以上
C. 降低了不到20% D. 降低了20%或以上
【答案】A
【解析】
第一步,本题考查经济利润问题,用赋值法解题。
第二步,总利润=单利润×销量,赋值2016年利润为10,销量为10。根据“每台产品利润提升10%”,可得2017 年每台产品利润为10×(1+10%)=11;根据“2017年全年销售这种产品的总利润较2016年增加了21%”,2016年总利润 =10×10=100,则2017年总利润=100×(1+21%)=121,根据总利润=单利润×销量,可得2017年销量=121÷11=11 。
第三步,2017年的销量比2016年增加(11-10)/10=10%。
因此,选择A选项。
对于赋值法,只要大家掌握基本的题型特征,在备考过程中认真巩固练习,就能在考试时解出答案。
行测干货数量关系之不定方程快速求解
一提到数量关系许多学生就纷纷抱头痛哭:“我的头好疼”、“太难了”、“学了不一定会,会了 不一定对”。

其实,小编想说的是对于数量关系的题目我们大家一定不要放弃,有些是我们能够迅速选出答案、性价比极高的题目。所以本 期内容就为大家介绍一种能够快速拿分的题型:不定方程(组)。
不定方程(组)在我们行测数量关系中可以简单的理解为所设未知数个数多于方程个数的题目。那不定方程(组)该怎么解呢?下面 我们就来学习三种解不定方程的绝招。

绝招一——代入排除
当题目中等量关系简单、求某未知数具体值时,可以采用代入排除的方法解不定方程。
【例】(2019河北)集贸市场销售苹果5元/个和火龙果3元/个,花光61元最多可购买这两种水果共多少个?
A.13 B.16 C.18 D.19
【答案】D
【解析】第一步:本题考查基础应用题,用方程法进行求解。
第二步:根据题意设购买苹果x个、火龙果y个,得到方程:5x+3y=61。
第三步:分析可知,要想购买水果总数最多,则需要更多的购买便宜的水果。因此要尽可能的多购买火龙果。根据题意,最多 购买19个水果。所以火龙果个数最多为19个。
将y=19代入,得:5x+3×19=61,解得x=0.8,不符合题意,排除;
将y=18代入,得:5x+3×18=61,解得x=1.4,不符合题意,排除;
将y=17代入,得:5x+3×17=61,解得x=2,符合题意,两种水果共17+2=19个。
因此本题选D。
绝招二——数字特性
当题目中的问题不能用代入排除法快速、直接求解时,可以考虑用数字特性进行求解。
数字特性包括:倍数特性、奇偶特性和尾数特性。
【例】(2020浙江)某会务组租了20多辆车将2220名参会者从酒店接到活动现场。大车每次能送50人,小车每次能送36人,所有 车辆送2趟,且所有车辆均满员,正好送完,则大车比小车( )。
A.多5辆 B.多2辆 C.少2辆 D.少5辆
【答案】A
【解析】第一步;本题考查基础应用题,用方程法进行求解。
第二步:根据题意设大车x辆,小车y辆,得到方程:2×(50x+36y)=2220。
第三步:方程化简后得:25x+18y=555。
由该式可知:
(1)555是3的倍数、18y是3的倍数,所以25x应为3的倍数,则x是3的倍数。
(2)555是奇数,18y是偶数,则25x是奇数,x是奇数。
综上可知,x是奇数且为3的倍数。
令x=3,得:25×3+18y=555,解得y≈26.67,不符合题意,排除;
令x=9,得:25×9+18y=555,解得y≈18.33,不符合题意,排除;
令x=15,得:25×15+18y=555,解得y=10,x+y=25,满足“某会务组租了20多辆车”,x-y=15-10=10辆。
因此本题选A。
绝招三——赋“0”
当题目中的未知数没有整数限制且所求为多个未知数的和时可用赋“0”法将某一未知数赋值为“0”进 行计算。
【例】(2016联考)木匠加工2张桌子和4张凳子共需要10个小时,加工4张桌子和8张椅子需要22个小时。问如果他加工桌子、凳 子和椅子各10张,共需要多少小时?
A.47.5 B.50 C.52.5 D.55
【答案】C

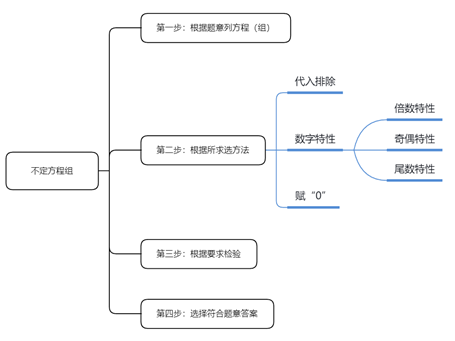
不定方程(组)解题方法思维导图:
2023年国考公告将出,华图教育为了华图教育回馈考生今年大力推出2023年国考系统提升班,不但有着强力的师资团队,还有着劲爆价格!
| 相关资料推荐 | |
| 2023国考乘风计划启航礼包 ¥0.1起 |
2023年国家公务员【高校专属】网课¥0 |
| 【教材+讲义+网课】23国考书课包 ¥159 | 23版国家公务员考试(行测+申论) 历年2本 ¥39 |
| 2023升级版国家公务员6本套+第17版名家讲义配套题库12本套 |
2023年国笔系统提升班 |
 |
|
上一篇:2023国家公务员考试内容?